Solar Eclipse Prime Page

Hybrid Solar Eclipse of -1779 Feb 12 (1780 Feb 12 BCE)

Fred Espenak

Introduction

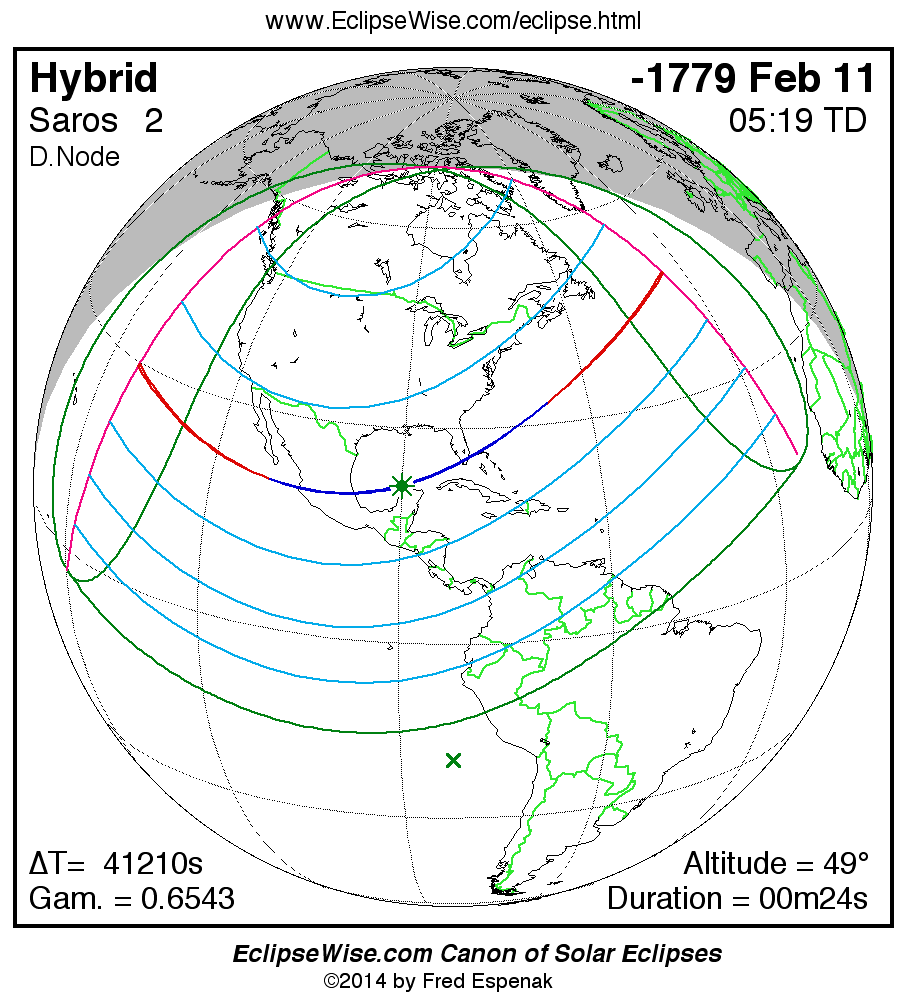
eclipse map

The Hybrid Solar Eclipse of -1779 Feb 12 (1780 Feb 12 BCE) is visible from the geographic regions shown on the map to the right. Click on the map to enlarge it. For an explanation of the features appearing in the map, see Key to Solar Eclipse Maps.

The instant of greatest eclipse takes place on -1779 Feb 12 at 05:19:03 TD (17:52:18 UT1). This is 4.2 days before the Moon reaches perigee. During the eclipse, the Sun is in the constellation Pisces. The synodic month in which the eclipse takes place has a Brown Lunation Number of -45786.

The eclipse belongs to Saros 2 and is number 61 of 73 eclipses in the series. All eclipses in this series occur at the Moon’s descending node. The Moon moves northward with respect to the node with each succeeding eclipse in the series and gamma increases.

The solar eclipse of -1779 Feb 12 is one of the rare hybrid solar eclipses. In this particular case the eclipse path starts out as annular. Further down the track it changes to total and then back to annular before the path ends. It is a very short hybrid eclipse with a duration at greatest eclipse of 00m24s. The eclipse magnitude is 1.0038, while Gamma has a value of 0.6543.

The hybrid solar eclipse of -1779 Feb 12 is followed two weeks later by a partial lunar eclipse on -1779 Feb 26.

These eclipses all take place during a single eclipse season.

The eclipse predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 41205.3 seconds for this eclipse. The uncertainty in ΔT is 2855.5 seconds corresponding to a standard error in longitude of the eclipse path of ± 11.93°.

The following links provide maps and data for the eclipse.

The tables below contain detailed predictions and additional information on the Hybrid Solar Eclipse of -1779 Feb 12 .

Eclipse Data: Hybrid Solar Eclipse of -1779 Feb 12

Eclipse Characteristics
Parameter Value
Eclipse Magnitude 1.00377
Eclipse Obscuration 1.00754
Gamma 0.65433
Conjunction Times
Event Calendar Date and Time Julian Date
Greatest Eclipse -1779 Feb 12 at 05:19:02.9 TD (17:52:17.6 UT1) 1071320.244648
Ecliptic Conjunction -1779 Feb 12 at 05:11:57.7 TD (17:45:12.4 UT1) 1071320.239726
Equatorial Conjunction -1779 Feb 12 at 05:31:19.0 TD (18:04:33.6 UT1) 1071320.253167
Geocentric Coordinates of Sun and Moon
-1779 Feb 12 at 05:19:02.9 TD (17:52:17.6 UT1)
Coordinate Sun Moon
Right Ascension20h44m13.8s20h43m46.7s
Declination-18°28'31.8"-17°51'04.7"
Semi-Diameter 15'59.9" 15'51.9"
Eq. Hor. Parallax 08.8" 0°58'13.5"
Geocentric Libration of Moon
Angle Value
l -4.3°
b -0.8°
c -17.2°
Prediction Paramaters
Paramater Value
Ephemerides JPL DE406
ΔT 41205.3 s
k (penumbra) 0.2725076
k (umbra) 0.2722810
Saros Series 2 (61/73)

Explanation of Solar Eclipse Data Tables

Penumbral Shadow Contacts and Extremes: Hybrid Solar Eclipse of -1779 Feb 12

Contacts of Penumbral Shadow with Earth
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
First External ContactP102:46:02.015:19:16.714°32.1'N129°54.0'W
Last External ContactP407:51:52.220:25:06.932°55.7'N043°49.1'W
Extreme Northern and Southern Path Limits of Penumbra
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
North Extreme Path Limit 1N103:39:38.016:12:52.703°10.9'S149°20.7'W
South Extreme Path Limit 1S106:58:25.219:31:39.815°26.4'N023°16.1'W

Explanation of Penumbral Shadow Contacts and Extremes Tables

Umbral Shadow Contacts and Extremes: Hybrid Solar Eclipse of -1779 Feb 12

Contacts of Umbral Shadow with Earth
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
First External ContactU103:56:21.516:29:36.229°24.7'N141°35.6'W
First Internal ContactU203:57:07.316:30:21.929°39.4'N141°40.4'W
Last Internal ContactU306:40:52.419:14:07.147°30.1'N034°57.6'W
Last External ContactU406:41:32.419:14:47.147°17.9'N034°58.1'W
Extreme Northern and Southern Path Limits of Umbra
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
North Extreme Path Limit 1N103:56:57.116:30:11.829°43.2'N141°36.2'W
South Extreme Path Limit 1S103:56:31.616:29:46.329°20.9'N141°39.8'W
North Extreme Path Limit 2N206:41:01.219:14:15.947°33.2'N035°02.3'W
South Extreme Path Limit 2S206:41:23.519:14:38.247°14.8'N034°53.4'W

Explanation of Umbral Shadow Contacts and Extremes Tables

Central Line Extremes and Duration: Hybrid Solar Eclipse of -1779 Feb 12

Extreme Limits of the Central Line
Contact Event Contact Time
TD		 Time
UT1		 Latitude Longitude
Extreme Central Line Limit 1C103:56:44.416:29:59.029°32.0'N141°38.0'W
Extreme Central Line Limit 2C206:41:12.419:14:27.147°24.0'N034°57.8'W

Explanation of Central Line Extremes Table

Greatest Eclipse and Greatest Duration
Event Time
TD		 Time
UT1		 Latitude Longitude Sun
Altitude		 Sun
Azimuth		 Path Width Central
Duration
Greatest Eclipse05:19:02.917:52:17.621°59.5'N097°50.5'E 49.0° 170.1° 17.2 km00m23.58s
Greatest Duration03:56:44.416:29:59.029°32.0'N218°22.0'E 0.0° 111.4° 40.4 km00m37.93s

Explanation of Greatest Eclipse and Greatest Duration

Polynomial Besselian Elements: Hybrid Solar Eclipse of -1779 Feb 12

Polynomial Besselian Elements
-1779 Feb 12 at 05:00:00.0 TD (=t0)
n x y d l1 l2 μ
0 -0.28311 0.61525 -18.4805 0.54870 0.00253 250.5306
1 0.54243 0.09323 0.0107 -0.00012 -0.00011 15.0007
2 0.00001 0.00010 0.0000 -0.00001 -0.00001 0.0000
3 -0.00001 -0.00000 - - - -
Tan ƒ1 0.0046773
Tan ƒ2 0.0046540

At time t1 (decimal hours), each besselian element is evaluated by:

x = x0 + x1*t + x2*t2 + x3*t3 (or x = Σ [xn*tn]; n = 0 to 3)

where: t = t1 - t0 (decimal hours) and t0 = 5.000

Explanation of Polynomial Besselian Elements

Links for the Hybrid Solar Eclipse of -1779 Feb 12 (1780 Feb 12 BCE)

Links to Additional Solar Eclipse Information

Calendar

The Gregorian calendar (also called the Western calendar) is internationally the most widely used civil calendar. It is named for Pope Gregory XIII, who introduced it in 1582. On this website, the Gregorian calendar is used for all calendar dates from 1582 Oct 15 onwards. Before that date, the Julian calendar is used. For more information on this topic, see Calendar Dates.

The Julian calendar does not include the year 0. Thus the year 1 BCE is followed by the year 1 CE (See: BCE/CE Dating Conventions). This is awkward for arithmetic calculations. Years in this catalog are numbered astronomically and include the year 0. Historians should note there is a difference of one year between astronomical dates and BCE dates. Thus, the astronomical year 0 corresponds to 1 BCE, and astronomical year -1 corresponds to 2 BCE, etc..

Eclipse Predictions

Predictions for the Hybrid Solar Eclipse of -1779 Feb 12 were generated using the JPL DE406 solar and lunar ephemerides. The lunar coordinates were calculated with respect to the Moon's Center of Mass. The predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 41205.3 seconds for this eclipse. The uncertainty in ΔT is 2855.5 seconds corresponding to a standard error in longitude of the eclipse path of ± 11.93°.

Acknowledgments

Some of the content on this website is based on the book Thousand Year Canon of Solar Eclipses 1501 to 2500. All eclipse calculations are by Fred Espenak, and he assumes full responsibility for their accuracy.

Permission is granted to reproduce eclipse data when accompanied by a link to this page and an acknowledgment:

"Eclipse Predictions by Fred Espenak, www.EclipseWise.com"

The use of diagrams and maps is permitted provided that they are NOT altered (except for re-sizing) and the embedded credit line is NOT removed or covered.